prepared during 1997 a zuppero, pat whitman (deceased), thomas k larson

Comets Appear To Be Herded Into Jupiter's Orbit And Erased By Mars Orbit

Approximately 150 dark and relatively close comets continuously occupy the region bounded rather sharply by the orbit of Mars and of Jupiter. We discovered that as we go out from the Sun, the probability of finding a comet in a given region of space abruptly rises at the orbit of Mars and abruptly drops at the orbit of Jupiter. The abruptness is unexpected.

A plot of the probability of finding a comet peridocally appearing in any given region between the Sun and Saturn reveals a donut, with a distinct hole starting at the orbit of Mars.

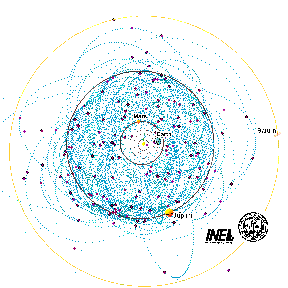
click for 70 k gif Figure 1 plots all the known comets closer than 10 AU (about the orbit of Saturn) and with periods less than 100 years (almost all the periodic comets), as seen from above the ecliptic plane. (Nearly all solar system objects orbit within 20 degrees of the ecliptic plane.) The larger diamonds represent the positions on October 5, 1996. The dots are equal time-interval points on the orbit of each comet. Each orbit is alloted 200 points, regardless of the orbital period. The density of the ensemble of orbit dots is roughly proportional to the probability of finding a comet in a given region, because the periods of the comets are mostly within a factor of 3 of each other.
The plot was designed for instructional purposes only, because the mere existance of the comets and their relatively slow orbital velocities is not a well known fact in the scientific community. A startling donut (torus shape) with a distinct "hole" in the center appeared unexpectedly.

Figure 2 displays the probability distribution with orbital period taken into account exactly. The distribution is of the projection of comet orbits on the ecliptic plane. Most of the comets have inclinations within 8 or 10 degrees of the ecliptic. This means their orbits are in a relatively thin disc in the same plane as the orbit of Earth.

Objects move the fastest near periapsis (closest approach) and slowest at apoapsis (most distant point). Plotting the orbits as equal time dotted points far more accuirately depicts the orbital characteristics than plots of elliptic orbits.

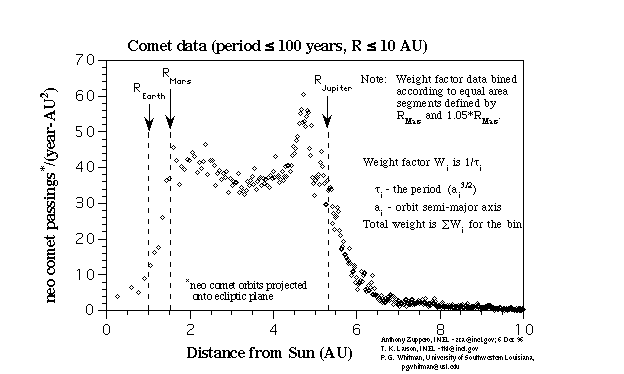
Figure 2. Radial Density plot.

At any given distance from the sun, the probability of finding a comet whose orbit projects into a fixed area of about 0.104 square A.U., is 1/200 of the value shown in the plot.

The area is a radial disc with the Sun as center. At Mars (1.53 A.U.) the inner boundary of the disc is the semi-major axis value of Mars orbit. The outher boundary is 1.05 times the Mars orbit.

The plot of Figure 2 is generated by summing each orbit point dot, weighted by orbit frequency, into equal area bins. A dot weight is assigned a value proportional to the amount of time a comet would have its orbit project into the given area of the ecliptic plane. This frequency is proportional to the reciprocal of the orbit period. The reference bin is the area from the orbit of Mars to 1.05 times the orbit of Mars. This is about 0.1037 square A.U. Each orbit is calculated with 200 points. So a value of "50" in the figure means 50/200 of an orbit.

The integrated "density of dots" as a function of distance from the Sun drops by a factor of about 5 just at the boundary of the orbits of the inner planets Mars, Earth, Venus and Mercury.

The distribution abruptly increases at the orbit of Mars and abruptly decreases past the orbit of Jupiter. The abruptness of the distribution inside the orbit of Mars is unexpected. The comet orbits do indeed pass deep inside the orbit of Mars. However, the pronounced ellipticity of comet orbits results in their spending only a small fraction of their orbital period closer to the Sun.

That the distribution should taper off as one moves inward, toward the Sun, is completely expected, perhaps due to physical and elastic collisions with the inner planets. The tapering past Jupiter is also expected, perhaps due to our observational bias. However, the abruptness starting at the orbit of Mars suggests some effect peculiar to Mars changes the distribution of visible comets. And the abruptness just past the orbit of Jupiter suggests Jupiter may be herding the comets into an orbit with periapsis near JupiterÕs orbit.

Proposed Mechanism for a Hole

Herding and evaporation could cause the apparent hole. A planet with significant gravity appears to herd comets into its orbit. Jupiter appears to do this. Mars, Earth, Venus and Mercury could also herd comets. Rapid evaporation of the volatiles would render a comet invisible. Each of the periodic comets are classified as comets because someone observed their tail. Comets that spend a significant fraction of their orbit within 2 or 3 A.U. evaporate in times small (of order 10,000 years) compared to the lifetime of periodic comets (of order a million years). This suggests that any comets herded within the orbit of Mars, or closer, become invisible because they evaporate their volatiles, leaving only the black, very low albedo material.

The albedo of comets is believed to be the darkest matter in the solar System. Dehydrated comets herded within the orbit of Mars, Earth, Venus or Mercury would either become invisible or be classified as near Earth asteroids. This would suggest that the comet ÒholeÓ consists of the the remnants of comets.

The number of spent comets within the comet hole could be large compared to the number of periodic comets. A periodic comet evaporates in a time of order 1 Million years. The orbit of the comet is stable for periods of order 10 Million years. [reference George Wetherill]] If the planets herd comets then any comets coming within the orbit of any of the inner planets become herded into a region where they are too close to the sun to keep their volatiles. Once devoid of volatiles, the objects can remain for a time as long as their orbits are stable. We are not aware of a good estimate of the lifetime of near earth asteroid orbits within the influence of the inner planets.

The existence of this "hole" provides us with a puzzle.