
(26K gif image).
AIAA 97-3172
33rd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit
July 6-9, 1997 / Seattle, WA
* Member AIAA
This paper is a work of the U. S. Government and is not subject to copyright in the United States.
During 1994 Eugene Shoemaker1 and Col. Pete Worden2 informed the INEEL that the Clementine probe returned a radar signal from the
 |
always-dark crater at the lunar south pole
indicative of water ice (see
Spudis).
(26K gif image). |
 Callisto
and at the
Callisto
and at the  poles
of the planet Mercury (60 K gif). NASA announced the discovery on 3
December 1996 to coincide with peer reviewed publication
(Nozette)3. The Lunar Prospector4, a
NASA Discovery mission, is scheduled for launch in September, 1997, with
a neutron spectrometer to measure the amount and extent of any water ice
within the first meter of the surface.
poles
of the planet Mercury (60 K gif). NASA announced the discovery on 3
December 1996 to coincide with peer reviewed publication
(Nozette)3. The Lunar Prospector4, a
NASA Discovery mission, is scheduled for launch in September, 1997, with
a neutron spectrometer to measure the amount and extent of any water ice
within the first meter of the surface.
(post-deadline reference:) Arnold and Watson first explored the theoretical possibility of ice at the lunar south poles.
(post-deadline reference:) Haloulakos reviewed the subject of nuclear thermal rockets and the performance of various propellants. His performance calculaltion code has been extensively validated by test data correlation. He computes the performance for a nuclear thermal rocket using CRYO H2, H2O, N2, NH3 and CH4 as propellants. He found that water could provide acceptable specific impulses at temperatures achievable with current materials.
Water from melted lunar ice could be used directly as a propellant. A steam rocket, with energy supplied by some external means such as a solar collector or nuclear reactor, would develop between 100 and 230 seconds of specific impulse (Isp) using the water directly as propellant.
Alternatively, lunar ice water could be electrolyzed into hydrogen and oxygen. After the gasses are compressed and cooled into liquid hydrogen (LH2) and liquid oxygen (LOX), they become premier chemical rocket fuel. The chemical rocket would develop much higher (in excess of 400 seconds) specific impulse.
The issue is whether to use the water directly, or to split and convert it into cryofuels. Landis5 and Zuppero6 examined this issue where propellant is abundant and the space transportation system is only limited by the total energy the system can give to the propellant. They showed that the optimum payload delivered per ton of launched hardware is greatest when the rocket exhaust velocity is about 2/3 the mission velocity. Since the mission velocity to escape the lunar gravity is about 2600 m/s, the optimum exhaust velocity is about 1730 m/s. This would imply a rocket specific impulse of about 175 seconds. A steam rocket with mixed mean outlet temperature of about 800 Kelvin would provide this performance.
One of the reasons for the Lunar Prospector mission is to verify theories suggesting that the lunar crater at the south pole contains in excess of a billion tons of water ice. If such a resource is indeed present, an appropriate nuclear-heated steam rocket propulsion system would provide near optimum performance.
The lunar gravity (about 1/6 that of Earth) forces the additional constraint that the rocket develop sufficient thrust to launch the initial mass of the rocket against that gravity. The thrust is directly proportional to the power delivered to the propellant, and inversely proportional to the specific impulse. The specific impulse is proportional to the square root of the propellant mixed mean outlet temperature.
The focus of this analysis is to determine the thrust-per-weight (specific power) and specific impulse (temperature) values that a nuclear-heated steam rocket must achieve if it is both to launch from the lunar surface and to use the lunar water most efficiently. (A solar heated steam rocket can not achieve the required specific power to launch from the lunar surface.)
This analysis connects specific power and specific impulse requirements to the required (minimum) nuclear reactor power per volume of nuclear fuel element and the required maximum temperature of the nuclear fuel elements.
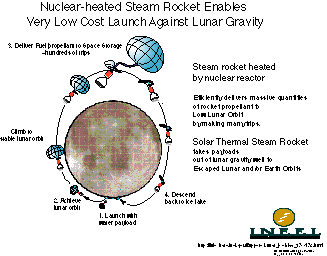 |
A lunar water-based system would deliver rocket propellant (water or
ice) to orbits around Earth. A nuclear-heated steam rocket (NSR) would
use water as propellant to launch the rocket propellant to orbit from the
lunar surface.
(24 K giff). |
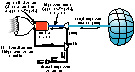 |
A nuclear-heated steam rocket engine (NSR) uses a nuclear reactor to
convert water propellant to superheated steam. A pump raises the pressure
of the water to about 3300 psi. Operation above the critical pressure avoids
a propellant phase change and allows operation at higher power density.
A rocket nozzle attached directly to the reactor converts the steam expansion
pressure into thrust. The rocket vehicle consists of the nuclear engine,
propellant water tank, nozzle, payload, and vehicle structure. Multiple
restart capability and high reliability, similar to nuclear submarine propulsion
systems, are essential.
(9 K giff). |
A simple schematic illustration of the nuclear reactor, propellant bladder, and nozzle is shown in Figure 1.
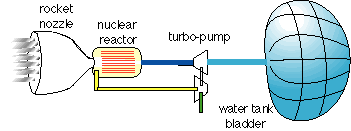
Figure 1. Steam rocket, nuclear reactor water heater and bladder water tank.
High cryogenic propellant tank fractions result from a combination of propellant vapor pressure, the need for thermal insulation, and optional micrometeoroid protection. Relative to other propellants, water has an anomalously low vapor pressure of less than 5 mm Hg at 1 Celsius. This permits a water tank in a low gravity to hold hundreds to ten thousand tons of propellant per ton of tank.
The dominant mass term for a water tank derives from the hydrostatic pressure due to lunar gravity and launch acceleration at the beginning of launch of a full propellant tank. The tank mass needed to contain the vapor pressure of very cold water adds only a small mass to the tank.
The mission architecture is composed of three segments. The first leg launches payload from the lunar surface to low lunar orbit. The second leg takes the payload from low lunar orbit to near lunar escape, which is the payload delivery point. (This leg could in practice be performed using solar thermal steam rockets. We chose a direct delivery.) The third leg returns the space water tanker from the lunar escape to the starting point on the lunar surface. A total propellant mass is calculated from the resulting mission delta-V.
The propellant tank mass depends on the total propellant for the three legs. We assumed a reasonable ullage factor of 5% (ullage is the residual water remaining in an oeemptyî tank). The total mass the rocket must lift from the lunar surface is the payload (water), propellant, propellant tanks, and the nuclear engine. The solution for propellant mass plus tank mass was performed iteratively in a spreadsheet.
We calculate the reactor power needed to develop sufficient thrust to lift this total mass against the lunar gravity at the lunar surface. This calculation gives the minimum power-per-mass of the nuclear reactor.
Lower temperature steam results in lower specific impulse. Too low a specific impulse (below about 150 seconds, corresponding to <800 K) will result in both unacceptably massive propellant use and unacceptably high required specific power.
Corrosion and oxidation of structural materials generally limit service life in high temperature steam. Although only limited long-term test data are available, one study [Berry] ranks several nickel-based alloys on oxidation and corrosion rates after 4000-hour exposure to 1000 K steam. The material loss rates at these conditions are acceptable. Considering NSR engine operating times are less than 20 minutes per mission, it is reasonable to anticipate higher but still acceptable material loss rates at somewhat higher temperatures.
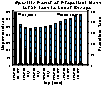 |
Figure 2: Power Per Unit Mass And Propellant Mass Vs Specific Impulse.
(9 K giff). |
The muddy water ice must be harvested, melted, and purified. All three steps can be accomplished using only low temperature process heat. It may prove advantageous to use some combination of mechanical and thermal processes. One way suggested by NASA to clean the water would melt the ice and boil the water in a near vacuum and at 1 degree Celsius. The vapor would be condensed into pure water and leave behind mud.
The energy required to heat, melt and boil the lunar ice to 1 Celsius is about 3 Megajoules of heat per kilogram of ice. This is a purely thermal process at 1 Celsius temperature. The reject heat from a nuclear electric generator such as an SP-100 service reactor can deliver this. For example, a 100 kilowatt electric generator would produce about 1 megawatt of waste thermal heat. This amount of heat would melt about 6,900 tons of water per year (1 Megawatt of thermal power, 5 days a week, 48 weeks per year). The Baseline NSR would deliver about 1123 tons to lunar escape orbit with this much water.
This suggests that the melting of ice is a relatively small issue.
Nuclear steam rocket system performance is evaluated using the following procedure. A desired payload ratio is first selected. Our payload ratio is defined as the tons of payload delivered to lunar escape orbit per ton of rocket engine. The rocket engine is assumed to consist of the reactor, turbopump, and nozzle. An initial estimate of propellant mass is made and the associated tank mass calculated. A fixed structural mass fraction is assumed. Using the total system mass, we calculate the power needed to lift the vehicle from the lunar surface at an acceleration of 1.5 times lunar gravity, including a gravity loss estimate. The propellant required to perform the round trip mission (launch, payload delivery to lunar escape, and empty vehicle return to launch site) is then determined. An iterative solution is required until the combined (propellant plus tank) mass values are converged. The result is the calculated power needed to achieve the selected payload ratio.
The resulting power level is the desired power per ton of reactor. For example, if we specify that we want 20 tons of payload per ton of rocket engine, we may calculate we will need to develop a rocket with specific power of 200 Megawatts per ton. From this we can estimate the required performance of the nuclear reactor. We rely on published9 particle bed reactor conceptual designs by Powell to correlate the required power-per-ton to nuclear fuel element power-per-liter.
| comment | low Performance NSR | baseline NSR | High Performance NSR | cryo option | units |
| Specific Power | 75.03 | 259.43 | 714.66 | 1295.36 | MW/ton |
| tons mass payload per tons engine | 4 | 20 | 60 | 120 | factor |
| Mass Ratio | 10.75 | 5.89 | 5. | 2.48 | tons at lift off per ton to L1 |
| tons mass tank per tons engine | 0.5 | 0.5 | 0.2 | 2 | factor |
| propellant mass | 40.96 | 102.74 | 252.08 | 186.48 | tons metric propellant mass |
| propellant density, rho | 1 | 1 | 1 | 1 | grams/cc or tons/cu.meter |
| propellant pressure | 0.088 200 | 0.088 200 | 0.088 200 | 10.000 000 | psi |
| propellant left in tank when tank is "empty" | 0.05 | 0.05 | 0.05 | 0.05 | fraction |
| total tank mass, kg | 137.48 | 461.98 | 151.33 | 1,256.51 | kg |
Performance evaluation calculations are performed using a spreadsheet. The spreadsheet reproduced as Table 1 summarizes the results for the four launch systems evaluated. In the "variable" column, variable names of input parameters are left justified and variable names of calculated results are right justified.
The nuclear systems evaluated are identified as low performance, baseline, and high performance nuclear steam rockets.
Power densities of 3.28 MW/liter have been demonstrated [Katscher]10 in inductively heated particle bed experiments. The power density achievable in the INEEL Advanced Test Reactor plate fuel is approximately 1.4 MW/liter. In both cases, atmospheric or low pressure light water at relatively low temperature is the coolant. Although conditions differ significantly, the demonstrated power densities suggest that 1.4 MW/liter power density and 75 MW per reactor ton should also be achievable.
The low performance NSR delivers 4 tons of propellant payload per ton of engine mass. This example launches more than 4 tons to low lunar orbit because it accounts for the propellant needed to finish the trip to lunar escape and return the launch vehicle. For 4 tons of payload, Table 1 shows we use 41 tons of propellant water at the lunar surface. We calculate the tank for this case to be about 0.2 tons. The empty mass of the launch vehicle is about 2 tons.
The Baseline NSR would need to reach a mixed mean propellant temperature of 1100 K. If technology permits operation at 1400 K, this will increase the specific impulse to about 230 seconds. The propellant mass would decrease to about 4.6 tons per ton delivered, instead of about 5.89 tons. The reduced mass ratios would permit about 40% more payload delivered.
Table 1 also shows that the tank and structure would be about equal to the rocket engine mass. The water tank parameters correspond to a relatively low technology. The tank would weigh about 0.46 tons with stainless steel walls 0.91 mm (0.036 in) thick. We assumed 40,000 psi yield strength (typical steel exceeds 100,000 psi), a factor of 5 safety margin, and a steel density of 8 g/cc.
A 2 ton rocket would deliver 20 tons of payload and use roughly 103 tons of propellant water.
The water tank for the high performance system would be a Kevlar composite. It would weigh about 0.151 tons. ItÃs walls would be 0.044 mm (0.017 in) thick. We assumed 150,000 psi yield strength, a factor of 5 safety margin, and a Kevlar density of 3 g/cc.
A 2 ton rocket using this 1 ton engine would deliver 60 tons of payload per engine mass, and require about 252 tons of water propellant.
The competing cryofuel systems have in their favor both good specific impulse (300 to 440 seconds) and high power-per-mass (of order 1,300 megawatts per ton). On the other hand, cryofuel systems require infrastructure to supply electrical energy to split the water into hydrogen and oxygen gasses, electrolysis devices, and a mechanical system to condense the gasses into the cryofuel propellants LOX and LH2. The electric generators and cryopumps require radiative heat sinks, which typically weigh as much as the other hardware.
We estimate the infrastructure mass for both cryofuel production and water production options.
The major system elements are a water ice melter and purifier, an electric generator, an electrolysis water splitter, a liquefier, a heat rejection radiator, and the launch rocket. The water ice melter energy requires at least two orders of magnitude less energy than splitting, so it is not a weight driver.
We modified their estimates because we consider their electric generator mass to be too optimistic. Their electric generator mass (35 tons) is about half of the total system mass. An electric generator weighing only 2.8 kg/kW (35 tons per 12.5 MW) should be compared to values used for Space Exploration Initiative studies, which bottom out at about 8 kg/kW. The INEEL SEHPTR spacecraft electric generator concept would weigh about 2300 kg to produce 40 kW, which is about 57 kg/kW.
If we use the optimistic value, we obtain a specific production capacity for cryofuel at the lunar surface of about 39 tons per year per ton of system infrastructure. Table 1 shows the cryofuel option delivers 1 ton of payload for each 2.45 tons of cryofuel. This gives a NET specific production of about 16 tons per year per ton of infrastructure.
The mass of the launch rocket is insignificant by comparison. The launch vehicle with a 1 ton engine and a 2 ton tank and structure can launch 180 tons per trip to lunar escape. Twenty trips could launch the entire yearly production of cryofuel.
The limiting infrastructure element is the cryofuel splitting and liquefaction system. On the one hand, a single, 3 ton cryo-propelled vehicle would deliver about 180 tons to orbit, several times per day. On the other hand, the rest of the system canÃt provide it with rocket fuel fast enough.
When a more realistic electric generator mass is used, which is of order 20 kg/kW, the 35 ton electric generator of the International Space University study becomes 250 tons, and the system mass becomes 285 tons. The specific production for 2300 tons per year using 285 tons infrastructure and 1 ton delivered for each 2.45 tons produced is 3.29 tons per year per ton of infrastructure.
|
Specific Production Capacity |
(Tons to Lunar Escape per Ton of Infrastructure) |
|
ISU IAM-90 electric power generator |
|
|
|
|
Kittel from NASA Ames gave us more data. The table shows that the cryofueled system to do the same job as a 6 ton nuclear heated steam rocket could weigh a thousand times more. The electric generator would weigh 1000 to 10,000 tons. The splitter and liquefiers would weigh between 400 and 4000 tons.
| Totals for cryofuel generator with 300 Kelvin heat sink | ||||
| delivering 14,000 tons per year to lunar escape | ||||
| (compare to 2 ton steam rocket system) | ||||
| Megawatts of Electric Power | ||||
| low power | higher power requirement | |||
| splitter | 11.99 | 11.99 | Megawatts | |
| LH2 liquefier | 104.68 | 162.84 | Megawatts | |
| LOX liquefier | 18.61 | 27.91 | Megawatts | |
| total | 135.28 | 202.74 | Megawatts | |
| TONS Electric Generator to achieve required power | ||||
| nukeBig | solar | nukemed | nukesmall | |
| tons/megawatt | 8 | 20 | 30 | 40 |
| tons | 1082.24 | 2705.60 | 4058.41 | 5411.21 |
| tons | 1621.93 | 4054.82 | 6082.24 | 8109.65 |
| TONS Hardware for splitters/liquefiers | ||||
| low mass | higher mass requirement | |||
| splitter | 179.84 | 179.84 | tons | |
| LH2 liquefier | 156.24 | 3472.00 | tons | |
| LOX liquefier | 86.80 | 763.84 | tons | |
| total | 422.88 | 4415.68 | TONS |
Last Update: 21 July 97
The NSR process consists of pumping the water directly into the steam rocketÃs tanks, instead of into the infrastructure to manufacture cryofuels. Only process heat is required.
The NSR system would use 2 units of mass to melt and purify water, and 1 unit of mass for the launch rocket. The energy required to melt ice or mud is at least an order of magnitude lower than that needed by the launch rocket, so these assumptions are considered reasonable.
The analysis shows that the Baseline NSR delivers about 20 tons of payload for each ton of nuclear rocket. The tank and structure add another ton to the system. The NSR system is limited by the number of round trips per day the 2 ton rocket can make. Assuming a 3 trip per day, 5 day week, 48 weeks per year schedule, the 2 ton rocket will deliver about 14,400 tons per year to lunar escape.
The total propellant water requirement is about 5.89 times as much, or about 85,000 tons of water. The water heater would need to deliver about 11 MW of low temperature process heat (at 1 Celsius).
The Baseline NSR system could deliver about 14,400 tons per year for a system mass of about 6 tons (2 for the rocket and 4 for infrastructure). The specific production is then about 2400 tons per year per ton of infrastructure
|
|
(Tons to Lunar Escape per Ton of Infrastructure) |
|
Baseline Isp and specific power |
|
The state-of-the-art in nuclear design and materials suggests that technology exists today to meet these nuclear reactor requirements for power per weight and specific impulse. The specific power requirement implies the NSR nuclear fuel must achieve 1.4 MW/liter. The specific impulse implies a mixed mean outlet temperature of 1100 K.
Calculations show the Baseline NSR infrastructure masses to be a factor between 150 and 720 lower than those of the cryo system.
A 2 ton Baseline NSR space tanker consisting of 1 ton engine and 1 ton tanks and structure could place about 20 tons per trip of arbitrary payload to a lunar escape orbit. Restart reliability of the reactor permits several trips per day.
The specific capacity of the Baseline NSR system is about 2400 tons of payload per year delivered to lunar escape from the lunar surface, per ton of infrastructure. The corresponding capacity for the cryofuel system lies between 3.3 and 16.
A steam rocket using water directly as propellant would consume about 2.5 times the propellant of its cryofuel counterpart for this payload delivery mission.
The cryofuel rocket compares poorly to the NSR because it requires an additional infrastructure to generate electricity in space, to split the water into hydrogen and oxygen using electrolysis, and to condense the gases into the premier cryogenic rocket fuels liquid oxygen (LOX) and liquid hydrogen (LH2).
A Baseline NSR could launch 14,400 tons per year using a single, 2 ton rocket supported by 4 tons of surface infrastructure. The Low Performance NSR would deliver 2880 tons (240 tons per month). The NSR principal processes require only thermal energy. The cryofuel system requires between 150 and 720 times more infrastructure mass to do the same job. This will translate into a proportionally lower mission cost.
2. Col. S. P. Worden, USAF, "Satellite on a Chip", Keynote Speaker Presentation at Eighth Annual Idaho National Engineering Laboratory Computing Symposium, 4-7 October 1994, Idaho Falls, Idaho.
3. S. Nozette, C. L. Lichtenberg, P. D. Spudis, R. Bonner, W. Ort, E. Malaret, M. Robinson, and E. M. Shoemaker, "The Clementine Bistatic Radar Experiment", Science, Vol 274, pp 1495-1498.
American Association for the Advancement of Science (1994) Special section
devoted to Clementine. Science, 266, 1835-1862.
* Internet References:
A complete
electronic version of article has been seen at:
http://www.fisica.edu.uy/hielolunar/articulo/
Lunar South Pole full images
Master Pointer list to URL for Clementine
(NASA JSC Johnson Space Center)collection of images
(Naval Research Lab)"The Deep Space Program Science Experiment (DSPSE), the first of a series of Clementine technology demonstrations jointly sponsored by the Ballistic Missile Defense Organization (BMDO) and the National Aeronautics and Space Administration (NASA ), launched in early 1994. Its principal objective is to space qualify lightweight imaging sensors and component technologies for the next generation of Department of Defense (DoD) spacecraft."4. Lunar Prospector, unpublished, Launch date 24 Sept 1997.
Lunar Prospector Information http://nssdc.gsfc.nasa.gov/planetary/lunarprosp.html
Lunar Prospector: Mission Management http://pyroeis.arc.nasa.gov/lunar_prospector/home.html
Lunar Prospector Construction on Schedule http://www.lmsc.lockheed.com/newsbureau/pressreleases/9627.html
5. G. Landis and A. C. Zuppero, "Optimum Rocket Transportation with In-Situ Propellants", Presentation at Joint NASA - Univ of Arizona Conference on Resources of Near Earth Space, Univ of Arizona, Tucson, AZ, 7-10 Jan 1991.
6. A. C. Zuppero and G. Landis, "Optimum Rocket Propulsion for Energy-Limited Transfer", Presentation at Joint NASA - Univ of Arizona Conference on Resources of Near Earth Space, Univ of Arizona, Tucson, AZ, 7-10 Jan 1991.
7. W. E. Berry, Corrosion In Nuclear Applications, (Wiley, New York, 1971), pp. 121-128.
8. Pratt & Whitney RL-10 A4-1, data sheet indicates 22,300 lbs thrust, 370 lbs mass, 451 sec Isp. Information available at: . http://www.pwfl.com/rl10.htm
9. J. R. Powell, H. Ludewig, and G. Maise, oeNuclear Thermal Propulsion Engine Based on Particle Bed Reactor Using Light Water Steam as a Propellantî, CONF 930103, American Institute of Physics Conference Proceedings 271, Tenth Symposium on Space Nuclear Power and Propulsion, Albuquerque, NM, 10-14 Jan 1993, pp. 579-582.
10. W. Katscher, " Coated Particle Fuel Element For Pressurized Water Reactors", Nuclear Technology, 35 (2): 557-580 (1977).
11. "International Asteroid Mission", International Space University Summer Study, International Space University; Parc d'Innovation, Blvd Gonthier d'Andernach, 67400 Illkirch-Graffstaden, France (1990).
Information available at:
http://isu.isunet.edu/Academic/SSP/isu90/IAM.html.
Watson W.D., Muray, B.C., and Brown,
Harrison* [*senior author], The Behavior of Volatiles on the Lunar Surface,
J. Geophys. Res. 66, 3033 (1961) (the first paper on the subject)
Haloulakos, V.E., "Nuclear Propulsion: Past, Present, and Future," presented at the Fifth Symposium on Space Nuclear Power Systems, the University of New Mexico, Albuquerque, New Mexico, 11-14 January 1988
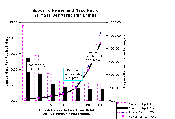 |
Engine Specific Power and Launched Mass as function of Engine-Specific
Payload, to Low Lunar Orbit. This calculation
delivers payload to Low Lunar orbit instead of to Lunar
Escape. This permits lower specific power, but trades system
complexity. The payload must be transferred in orbit to another vehicle
that takes it to Lunar Escape, and one must launch between 1.4 and 1.6
times as often to make up for the smaller mass placed into orbit.
(9 K giff). |
format mod 971129 a zuppero