
physics of rocket systems with
separated energy and propellant
Anthony Zuppero
Idaho National Engineering and Environmental Laboratory
31 december 1998
This describes the physics of rocket systems where the energy comes from one source and the propellant comes from another. Nuclear thermal rockets using liquid hydrogen propellant and electric ion engines are examples of this kind of rocket system.
When the payload originates in space and the rocket propellant also originates in space, then one only needs to pay for launching the rocket system. This has become the case of interest because water ice or hydrogen has been discovered on the moon. Water or hydrogen can be rocket propellants. Solar thermal rockets and nuclear-heated thermal rockets can use water propellant from Lunar, asteroidal or cometary sources. The sun or nuclear energy supplies the energy. Resources already in space would supply the propellant mass. The engineering parameter to be determined is the choice of propellant exhaust velocity that delivers the largest payload, or that delivers the payload fastest, or that uses the least energy to deliver a given payload at a given mission velocity. The rocket system design question is: how do we use the propellant?
What is the optimum exhaust velocity?We assume we launch just the rocket system, without propellant or payload. Once in space, the system would dock with a propellant station and fill the propellant tank with propellant whose cost is much less than that of launching it. The rocket system would also take on payload in space.
The only option available to the designer is to choose the propellant exhaust velocity.
We can only deliver a fixed amount of energy to the propellant. Material properties and mission thrust profiles constrain the energy delivered to the propellant to be a fixed value, namely, as much energy as we can generate during the time we have and using the heat or energy source we have. We try to design the fixed amount of energy to be as large as we know how to design. We always try to deliver as much energy as we can.
The fundamental question is the choice of propellant exhaust velocity. If we choose a high velocity then we will deliver the energy to a small amount of propellant, and we will only need a small amount of propellant. If we choose a low velocity then we will need a large mass of propellant. Conventional rocket science abhors results which demand a large amount of rocket propellant. The conservation of energy mandates that:
E = 1/2 M V2where E is the energy delivered to the propellant, M is the propellant mass, and V is the propellant exhaust velocity. Which velocity is the best?
“Highest velocity” is the rocket scientist’s incorrect answer.
We will show below that the correct answer is some intermediate value. The incorrect answer “highest specific impulse” is the equivalent to putting all the available energy into as small a propellant mass as is practical. The highest energy per mass means the highest specific impulse.
However, if we must launch the propellant with the rocket, then this whole exercise is irrelevant.
This question of exhaust velocity was irrelevant and academic until 3 sept 1998, when Binder, Feldman et al. published the Lunar Prospector data. The Lunar Prospector data suggest the possible existence of up to 1e10 tons (ten billion) of relatively pure ice veins at these moon poles. INEEL published system calculations showing how to deliver kiloton quantities per year of ice or water from these poles to a lunar escape orbit, or to a stationary orbit. The possibility of a gas station in space makes this question of “what exhaust velocity” relevant. The specific velocity, Vsp, is directly proportional to the specific impulse Isp. Specific impulse is a measure of propellant exhaust velocity.
Vsp = Go * Isp"V" or "Vsp" is the specific velocity, which is the equivalent exhaust velocity of molecules going out the back of the rocket. Go is the gravity constant at the surface of the Earth, with value about 9.8 meters per second per second. Isp is measured in "seconds." For example, a specific impulse of 450 seconds means the exhaust velocity is about 4,410 meters per second. This is the exhaust velocity of the RL-10 engine, which runs on liquid oxygen (LOX) and liquid hydrogen (LH2). Ion engines with 8000 second specific impulse deliver an exhaust velocity, Vsp, of about 80 km/sec. The specific impulse of the nuclear heated, liquid hydrogen propellant rocket tested during the late 1960's (called NERVA) demonstrated about 800 seconds Isp, or about 8 km/s Vsp.
The objective, then, is to determine:
What specific velocity (impulse) should one try to achieve, given that one wants to deliver the largest payload, or to go fastest, or to use the least energy to deliver a given payload?Note that this objective does NOT say “minimize the amount of propellant taken on at the gas station.”
Simple, Few-Line Derivation
Only a few lines of simple algebra are needed to derive the principle.
Suppose we have a rocket system that has a payload, P, a propellant mass,
M, and a rocket ship with mass S. Some energy source delivers energy
E to the propellant mass M. The propellant exhaust velocity is V.
The objective is to find the best propellant exhaust velocity, V, to deliver
the payload.


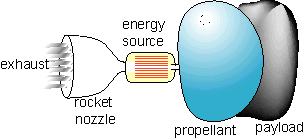
Figure 1. A simple rocket delivers a payload by heating a propellant mass into a gas, which it expells out the nozzle, producing thrust. The ship consist of the engine, structure, and propellant holding system.
The perfect rocket nozzle converts the random motions of a high pressure exhaust gas at the throat of the nozzle into low pressure gas with all the molecules moving in one direction, namely directly out the back of the nozzle. The rocket energy source deposits all the energy E into the propellant.
The conservation of energy relates the kinetic energy of the propellant to the velocity, E = 1/2 M V2
The conservation of momentum gives the rocket equation, which relates the final velocity, delta-V, as a function of the initial rocket system mass and final rocket system mass.
misson velocity = V * natural logarithm of (mass at start / mass at end)The initial mass is the payload, ship and propellant. The final mass is just the payload and ship.
delta-V = V * ln ( (S+P+M) / (S+P) )Substituting 2*E/V2 for M and assigning the constant k = 2*E/(S+P), the delta-V relation becomes:What is the value of V to make this equation give the largest delta-V?
delta-V = V * ln ( 1 + k / V2 )To get the optimum, find the V that makes the expression on the right have a maximum value. One can get a three digit approximation to this trancendental equation with a simple pocket calculator and 15 minutes of iterative guesses. One solution method defines a dimensionless variable x2 = V2/k and optimizes the dimensionless function f(x)=x*ln(1+1/x2). The optimum "x" is approximately 0.504976....... The correct answer is that for any value of k, the optimum V is approxmately 2/3 delta-V, the mission velocity:
optimum Vsp ~ delta-V * 0.6275.....This means that the best propellant exhaust velocity is about 2/3 of the missoin delta-V (.6275 is approximately 2/3). This optimum velocity gives a mass ratio of about 4.92, which means that the propellant mass is about 3.92 units when the payload and ship mass is 1 unit.
The rocket scientist’s incorrect answer is “largest V.” This would be the equivalent to specifying the highest value for specific impulse. Letting V go to infinity in this equation gives zero rocket performance. The performance scales inversely as V for large V.
The other incorrect answer is “smallest V.” Letting V go to zero also yields zero rocket performance.
This simple, “back of the envelope” calculation has all the energy going into directed motion of the exhaust molecules. In practice only some fraction is available for specific impulse. The remainder of the energy can be wasted in many ways, such as in heat, wasted in an electric generator process, tied up in molecular vibrations and electronic excitations, or in random motions of the gas resulting from an imperfect nozzle that is not infinitely large.
The missing tank is the most serious deficiency in this simple calculation. One needs a tank to hold the propellant.. Ice might be its own tank. However, one always needs some tank, and the tank mass is proportional in some way to the mass of the propellant it contains. One must launch the tank, even though one does not launch the propellant. When one includes a tank term with mass proportional to propellant, the effect on the optimum velocity is not obvious.
Derivation Including Tanks and Ullage.
A more complete derivation includes the tank mass and the fraction
of propellant left in the tank when the rocket is finished, called ullage.
The desired expression = Payload per Launched_Space_Truck_Mass
[E/S] == Energy E that a given mass of space tanker ship, S,
can deliver to
Exhaust Mass, M, with
specific Velocity V == Vsp.
V = Vsp is the exhaust velocity, and is the metric definition of specific impulse.
Exhaust mass M and [E/S] are completely separate entities, independent of each other.
The payload per launched mass depends on the energy per weight ratio of the ship [E/S] , and the exhaust velocity V. The mission velocity is the mission delta-V that the rocket system must achieve. The relationship between payload and the two variables [E/S] and V are derived starting with the rocket equation:
![]()
Where
![]()
and in symbolic terms
![]()
where
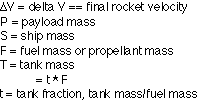
t == tons tank per tons of fuel in full tank
u == ullage = fraction of fuel left in tank when tank is "emptied"
u*F == Leftover_Fuel
The rocket equation thus gives:
![]()
where ![]() , d is the ratio
of mission velocity to specific velocity.
, d is the ratio
of mission velocity to specific velocity.
The relation expands to:
![]()
which simplifies somewhat to
![]()
The next relationship shows the critical difference between chemical rockets and rockets with separate energy and propellant sources. The only propellant velocity that contributes to thrust is the propellant exhausted out the rocket nozzle with velocity component directed opposite to the force vector. This component of energy is defined as E. The relation requires the designer to be able to calculate the E representing the kinetic energy associated with specific impulse. For a steam rocket operating at 1100 Kelvin and starting with liquid water propellant, calculations suggest that this E is of order 70% of the energy delivered by the heat source. The thrust time for Mars mission thermal rocket is measured in tens of hours and the power in tens to hundreds of megawatts. For ion engines the heat source converts between 10% and 20% of the energy into electricty, and about 50% of the electricity apprears along the thrust vector. The thrust time for such an electric rocket is measured in years and the power in terms of Megawatts. The only energy of interest is the energy associated with the velocity componet along the thrust vector:
![]()
and this gives:
M = ![]()
Note the (1-u) term accounts for the fact that the fuel still in the tank when the thrusting is over does not consume any of the rocket energy.
We now calculate the payload per launched mass. We divide the (P+S+T) term by the launched mass, which is the ship (energy source, structure, rocket nozzle) plus its Tank, and substitute the expression for exhaust mass, M, to give:
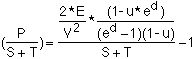
Substituting the tank term, noting that the tank is some fraction of the propellant, and substituting the exhausted mass term, gives:
![]()
Collecting terms gives:
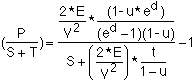
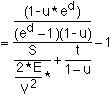
The resulting expression is one form of the desired result:
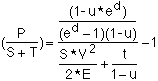
The next step replaces the dummy variable d and casts the relation in terms of Energy-per-Ship:
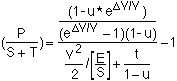
Payload/Launched_Mass =
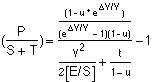
A related derivation leads to the conclusion that a single, optimum value of Vsp maximizes the payload, or minimizes the energy required to deliver the payload, or maximizes the resultant delta-V. This derivation is given in Appendix I.
Simplest Case: Perfect Tanks and Zero Ullage
The simplist case where tanks weigh nothing (t=0) and ullage is zero (all fuel used) reduces to
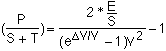
This function has a maximum when the specific velocity, V, is about 2/3 the mission velocity delta_V. The performance is directly proportional to the Energy deliverable into the propellant.
This physics exercise replaces
"maximize specific impulse"
with
"maximize energy into the propellant velocity vector along the thrust vector"
The starting point is from an Earth orbit with perigee of about 1.3
earth radius and apogee of about 120 earth radius. This is about a one
month orbit (same as moon period) and confines the rocket system to a path
outside the debris zone near Earth.
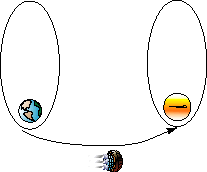
An impulsive thrust in the region of perigee must achieve a V_infinity of about 4000 m/s to achieve a Hohman transfer. Thrusting in the region of the perigee to develop a delta_V of about 840 m/s will result in both Earth escape and the required 4000 m/s V_infinity (a C3 of about 16 km squared per second squared).
At Mars, the vehicle is moving about 4000 m/s too slow (approximately the Hohmann transfer to capture at Mars). A propulsive thrust at Mars closest approach of about 1470 m/s causes a capture about Mars. The periapsis will be about 1.1 Mars radii, and apoapsis of about 120 Mars radii.
Note that the vehicle uses its rocket propulsion to achieve capture at Mars, not aerobrake. Dr. Buzz Aldrin, Apollo 11 Astronaut, said he doesn't like the aerobrake maneuver at Mars. A miscalculation of the height and density of the atmosphere can result in either no capture or immediate crash into Mars.
The total delta_V is about 2310 m/s. This is nearly the minimum delta_V
to get from Earth vicinity to Mars vicinity.
Figure 1 shows the payload per launched rocket system mass as a function of the specific impulse (seconds) and as a function of tank fraction. The figure shows that the performance P/(S+T) has a definite peak and is a strong function of the tank fraction.
In Figure 1 the curve with a tank fraction of about 1/1000 ton bladder tank per ton propellant, (fourth curve from the top, shown as 1.00E-3) has an optimum Isp of about 310 seconds with performance of about 160 tons of payload per rocket vehicle. This tank fraction is appropriate for water bladder tanks. The specific impulse is appropriate for hydrocarbon-LOX engines. The Isp below about 200 seconds is appropriate for an achievable steam rocket generating mixed mean outlet steam at about 800 Kelvin. At 149 seconds Isp the performance drops to about 130 tons per ton, which is close to the 160 optimum.
Figure 1 also shows that when the tank fraction is appropriate for liquid hydrogen propellant (LH2), with value 1/10 ton tank per ton propellant, the performance is an order of magnitude lower. This is the bottom curve. The performance peaks at some specific impulse about 1500 seconds. The performance at 924 seconds Isp is about 20 tons payload per ton rocket vehicle.
The nuclear rockert scientists using LH2 propellant correctly insisted on increasing the specific impulse to improve performance. However, if water becomes available, then the tank can weigh a smaller fraction of the propellant, and the rocket will perform an order of magnitude better with less than 1/3 the specific impulse and at less than half the operating temperature.
Table 1 shows some of the data used to specify the relevant tank fractions and engine types for the figure. The tank fraction values are those considered to be at the limits of realistic tank performace for the category of propulsion (steam, cryo, LH2 and ArcJet/Ion). Note that the higher specific impulse propulsion regions (cryo, LH2, Arcjet/ion) always perform at least about an order of magnitude worse than that of steam.
Table 1 Data
| Steam | Cryo | |||||||
| Isp 149 | Isp 215 | Isp 310 | Isp 446 | |||||
| tank | 5.00E-03 | 78.0 | 113.7 | tank | 1.00E-01 | 14.1 | 22.0 | |
| tank | 2.00E-04 | 197.5 | 205.4 | tank | 2.00E-02 | 56.6 | 70.9 | |
| P/(S+T) | ||||||||
| LH2 | ArcJet / Ion | |||||||
| Isp 535 | Isp 924 | Isp 1109 | Isp 3312 | |||||
| tank | 1.00E-01 | 14.2 | 22.7 | tank | 1.00E-01 | 25.0 | 21.1 | |
| tank | 2.00E-02 | 74.3 | 67.3 | tank | 2.00E-04 | 71.9 | 25.6 |
Table 1 Tabular P/(S+T) data corresponding to the curves in Figure
1. For example, the first entry shows that the P/(S+T) is about 78.0
for an Isp of 149 seconds for a tank fraction of 5.0E-3. This tank fraction
is the equivalent to a tank holding 200 tons propellant per ton tank. This
corresponds to what more conservative steam rockets can achieve.
An example shows that rocket system with performance parameters like that of a steam rocket would produce nearly the optimum specific impulse for transporting the largest payload from a high Earth orbit to a high Mars orbit. Higher specific impulses (600 - 900 seconds) such as are achievable using liquid Hydrogen propellant typically result in at least an order of magnitude poorer performance.
The payload per unit mass of the un-fueled space vehicle was derived as a function of the mission delta-V, exhaust specific velocity (equivalent to specific impulse, Isp), the specific energy [ E ] (total energy a given mass of rocket can give to the propellant), and as a function of the tank fraction and ullage (left over propellant).
Question: What is the optimum Vsp to get the largest delta_V,
expend the least energy E, and/or deliver the largest Payload?
Answer: The same value of "delta_V /
Vsp"
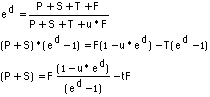
And substituting...
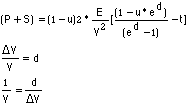
Gives....
![]()
The left hand side is [Kinetic Energy into payload and ship] / [Energy into propellant]
The right hand side is just a dimensionless function Fcn (d, t, u) of
three dimensionless numbers (d,t,u). Only d is related to the optimum Vsp.
When the value of d is found that maximizes the function, then d=delta_V/Vsp
gives the optimum Vsp.
Maximizing the term ![]() which is Fcn (d, t, u), maximizes the term
which is Fcn (d, t, u), maximizes the term ![]() .
This maximizes P+S, or it maximizes delta_V, or it minimizes E.
.
This maximizes P+S, or it maximizes delta_V, or it minimizes E.