Water Ship to take 50,000 Tons back to orbits around Earth
< first document: 6/26/2010 3:19:31 PM A Zuppero, commissioned and paid for by Paul Sturrock.
back to neofuel.com
back
to neofuel.com/space
This document sketches estimates of the masses for the concept of a
water ship space
vehicle needed to deliver 50,000 tons of payload to a barely captured
orbit
around Earth from a generic near earth object "Deimos, Moon of Mars".
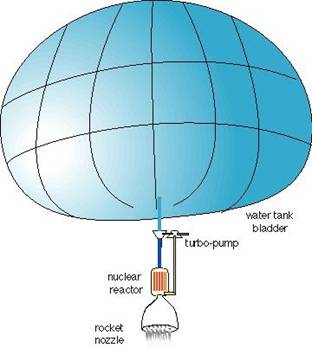
Strategic Intent:
Imagine an ice cave inside some near Earth object, with
water dripping into pools and collection tanks.
Imagine a Space Shuttle nudging a water balloon as big as the 85 yard line of a football field,
silently,
through the black night of space.
Imagine someone in orbit around earth getting hold of
five long train loads of anything,
like 50,000 tons of steel or water,
to use for making space ships,
rocket fuel propellant, shielding,
solar power satellites,
really big space ships,
and all kinds of imaginative,
spacey things.
Imagine the Shuttle uses water in steam rockets heated by small nuclear reactor heaters. Imagine a nuclear water heater melting the ice cave.
50,000 tons is about as much mass as 400 Space Shuttles all at once.
The missions assume there is "ice" readily accessible on Deimos. An "ice cave" is assumed to be created by heating the ice using a nuclear reactor. One could also have chosen one or more the near Earth comets for the ice. The comets are sure to have ice but have a minimum mission delta_V to capture in excess of about 4500 m/s. Deimos is claimed to be a prime candidate for having ice, and its minimum mission delta_V is about 2200 m/s.
Mission "delta_V" matters exponentially. The "rocket fuel" propellant required is proportional to the exponential of the delta_V per propellant exhaust velocity. Doubling delta_V can make the mission impossible (to engineers, not physicists or space cadets).
If there is mineralized water on the near earth asteroids (NEAs), this "Deimos" mission could be a good estimate of missions to get NEA resources
The vehicle consists mainly of engines and "water balloon" tank. A "water ship" nudges a water balloon and a payload through space using a steam rocket heated by some heater such as a nuclear reactor.
The mass of the water propellant used in orbital maneuvers is also estimated.
These estimates provide a reference nominal water ship and mission. We want to know how much water heater power will be required, how much tank mass is needed. These are the heaviest elements by a large margin. A summary of the mission can be deduced by examining the input/output table below.
|
|
Input |
|
|
|
|
50 kT, Slo Thrust credible engines, dV 50% margin, E_liq-g fixed |
|
|
|
margin_dv |
% |
margin over minimum mission delta_V |
|
|
ullage |
percent of "fuel" left over |
||
|
tankF |
tank mass per fuel propellant mass, with margin |
||
|
Isp |
specific impulse |
||
|
Pld |
payload |
||
|
Eng |
tonnes |
engine --heater with its structure |
|
|
nozfact |
nozzle efficiency factor |
||
|
slowtime |
hours |
thrust time |
|
|
|
|
|
|
|
|
|
|
|
|
|
Output |
|
|
|
dV |
3,234.54 |
m/s |
mission delta_V |
|
|
24.89 |
tonnes |
tank |
|
bareship |
tonnes |
empty ship |
|
|
fuelpropellant |
fuel propellant |
||
|
|
299,030.63 |
starting mass |
|
|
|
15,137.86 |
tonnes |
Margin excess propellant at destination |
|
|
0.005214814 |
g |
acceleration relative to earth = 1g |
The first step is to compute a tank mass to hold the water. The tank is more like a thin Mylar balloon used for helium filled toys, but larger. Most of the tank mass is used to contain the water "weight" during accelerations rather than in containing the water vapor pressure to keep the water liquid. The computation is iterative, so one must guess and iterate.
Then one computes the ship mass, with assumptions about the engine power needed and mission delta_V penalty due to slow maneuvers. With a few iterations one gets two kinds of ship, an "engine-rich" ship that is efficient at taking advantage of Oberth maneuvers, and an "engine-poor" ship that uses more water but far less nuclear rocket power and can incur a 50 % penalty on some of the propulsion maneuvers.
I choose the "engine-poor" mission because it takes less engines, which are expensive, rather than "engine-rich", which would save water, which we have lots of.
For the sake of calculations, the other parts of the vehicle such as struts and structures and navigation are all lumped into the "engine" mass.
The result is the mass budget to deliver 50,000 tons from Deimos to a highly elliptical earth orbit (HEEO).
Note that when I quote something like " 147.89 tons" it has all the extra significant figures so you can find the number in the tables.
|
bareship |
147.89 |
tonnes |
empty ship |
It really means " about 147, maybe 150 ".
One must realize that I am only getting estimates, not hard numbers, because I am only showing that the missions are relatively simple and that the masses are in the range of what we might actually do.
Also, I used coplanar, circular Earth, Mars and Deimos orbits for simplicity. When I do that the delta_V's are a bit smaller than the real ones. This reduces the complexity of the calculations. To minimize the errors induced by using slightly idealistic delta_V's I add "margin" in the entire mission delta_V.
To
assure
mission margin, I took the entire mission delta_V
and increased it by 50%. An orbital maneuver simulation had shown that
50%
increase in delta_V can result when a thrust that is supposed to happen
at the
closest approach to a heavy object, like the Earth or Mars, takes 10
hours
instead of 20 minutes. For example, if the thrust takes more than days,
the full
"V_infinity" must be achieved, which can be 9 km/second for missions
from near earth comets. If a thrust occurs at periapsis (closest
approach) the delta_V can
be ~3 km/s. The "3" is doable, the "9" is not, using a steam rocket. If
one were using liquid hydrogen instead of steam, the mission would
still be marginal because of several other issues, including the tank
issue, even though the delta_V penalty could be smaller. Liquid
hydrogen requires tanks that can weigh 1%-2% of what they hold. One can
see how the delta_V penalty for using to low a rocket power
can be severe. A more conservative way would be to increase the
delta_V's of
only the critical maneuvers. However, space is mean.
|
margin_dv |
50 |
% |
margin over mission delta_V |
Mission designers can detail the mass budgets and orbital maneuvers quite accurately. We should get the real numbers from them, except that the celestial objects are moving all the time so the maneuver delta_V are constantly changing.
Result
The result detailed below is that a "small" water ship with mass (~ 150 tons) a little above that of a space shuttle (~ 120 tons) would deliver about 50,000 tons of water to HEEO, or maybe to LEO, every orbital period, e.g. about every 2 years (~ 4 years and longer for comets). The nuclear reactors would be used so few hours (~ 20 hours per trip) they could last a century. They would be obsolete before that, like computers.
The table entries below are copied from the spreadsheets ( excel mission spreadsheet, excel tank spreadsheet ).
-------------------------------------------------------------
Tank, after couple of iterations
The tank must hold about 300,000 tons of water,
where 248,877
tons is propellant and 50 ktons is payload.
The tank calculation estimates the mass of a container needed to hold the contents pressurized enough to keep it liquid and the separate mass of container needed to hold the pressure of a column of its contents while being accelerated at some "g" value.
The result for this 50,000 ton payload depends on the propellant mass needed, which is about 300,000 tons.
|
fuelpropellant |
248,882.74 |
tonnes |
fuel propellant |
and on the acceleration, which is about 0.005 g (Earth surface is 1.0 g)
|
0.005214814 |
g |
acceleration relative to earth = 1g |
One can see in the tank calculation below that the tank can weigh as little as 0.000036742 of its water content, about 0.003,6%. This would be a water balloon, not a tank. Usually one does not make such a thin-walled tank. Usually one is in the crushing acceleration of the Earth surface. However, the water ship is in space.
Usually one "armors" the fuel or propellant tanks to keep them from being ruined by the micro-things that hit the tank from space. The armoring problem is solved by using some margin mass to wrap the thin propellant tank in more, thin "tanks" outside the propellant tank. The outer barrier just holds either ice or space dirt as armor. I used 0.01 % instead of a thinner 0.0036 % tank mass / fuel mass percentage. Margin always wins.
The result is curious in that the tank mass to hold the hydrostatic pressure of 300,000 tons of liquid in a 5 milli-g acceleration is about 4 or 5 times the mass needed to contain the vapor pressure of the liquid.
Excerpt from tank spreadsheet:
|
kgHydro |
kg |
tank mass for Hydrostatic = acceleration term |
|
|
thickHydro |
inches |
thickness of tank for hydrostatic pressure = acceleration |
|
|
kgPressure |
kg |
tank mass for Vapor Pressure term |
|
|
thickPressure |
inches |
thickness of tank for vapor pressure containment |
One clever person asked what if there were no tank at all. That would be like a comet, which has no tank at all. I think that would work. We would ship an ice cube instead of a water balloon. We would cover the ice with dust, like a comet.
Excerpt from tank spreadsheet file input/output part:
\ tank-C Deimos 50 kT water ship 2010.06.28_0739.xls
|
|
|
|
calculates tank mass to hold propellant in given g |
|
|
|
|
|
|
|
input |
|
date: 2010.06.28 7:38 AM |
|
|
Kevlar foil tank for H2O 50kt payload, 300 kT total |
|
|
|
propMass |
tons metric |
FIRST GUESS at propellant mass |
|
|
YStress |
214,000.00 |
psi |
yield stress of tank wall material |
|
propRho |
g/cc or tons/cu.meter |
propellant density, rho |
|
|
propPatm |
0.10 |
psi |
propellant pressure |
|
tankRho |
1.50 |
g/cc, tons/m^^3 |
tank mass density |
|
SafetFact |
3.00 |
factor |
safety factor for stressing tank, >>1 is very safe |
|
NGeesTank |
5.21E-03 |
fraction |
number of G's tank will experience when ful, 1 Gee - 9.8 m/s/sl |
|
Ullage |
fraction |
ullage, propellant left in tank when tank is "empty" |
|
|
gagelimit |
0.01 |
inches |
minimum thickness of material, gage limit |
|
|
|
|
|
|
|
|
|
|
|
|
output |
|
|
|
tFactor |
<<1 is very good |
tons tank mass per ton propellant |
|
|
tankThick |
inches |
total tank thickness: conservative: sum of pressure & hydro term |
|
|
kgTank |
kg |
total tank mass, kg |
|
|
PropPerTank |
>>1 is very good |
tons propellant per ton tank |
|
|
propVol |
3.26E+05 |
m^^3 |
propellant volume |
|
tankDiam |
8.54E+01 |
meters |
diameter of tank if it were sphere |
|
|
|
|
Heidenreich changes 19990417 |
|
kgHydro |
8.97E+03 |
kg |
tank mass for Hydrostatic = acceleration term |
|
thickHydro |
1.37E-02 |
inches |
thickness of tank for hydrostatic pressure = acceleration |
|
kgPressure |
2.06E+03 |
kg |
tank mass for Vapor Pressure term |
|
thickPressure |
1.18E-03 |
inches |
thickness of tank for vapor pressure containment |
---------------------------
engine masses
The nuclear engines are just nuclear reactors that would heat the water to a high enough temperature to generate a specific impulse of about 190 seconds. This temperature is somewhere near 800 Celsius. The claimed power per mass of the engine and the operating temperature determines how credible the engine is. If we claim the engine only needs to generate 100 Megawatts per ton engine at "only" 800 Celsius it is credible. About ~ 1100 Kelvin temperature is extremely hot for a water cooled nuclear reactor. By comparison, the RL-10 rocket engine that runs on liquid hydrogen and liquid oxygen generates about 1,300 Megawatts per ton, or about 13 times higher peak power. The NERVA tests indicated that the liquid hydrogen cooled nuclear rockets operating at about 2500 Kelvin could generate 300 megawatts per ton. Our "100" number is at the low end of the quoted power densities. I included an engine mass estimate for 300 megawatts per ton in the spreadsheet just to get a feel for margin.
The 121.42 ton engine mass is for an engine-poor mission, which uses relatively more water propellant than if we used more engines. We have lots of water.
The 40.47 ton mass is for the same, slow mission using a high performance engine. We do not have a lot of money to develop a high performance engine.
|
nuclear engine mass |
|
|
|
1.21E+10 |
watts |
(copy of ) thermal engine power |
|
1.00E+02 |
MW/tonne |
(copy of ) specific power "easy" to believe/achieve |
|
3.00E+02 |
MW/tonne |
(copy of ) specific power claimed at INL |
|
121.42 |
tonne |
engine mass |
|
40.47 |
tonne |
engine mass, optimistic |
The 147.89 ton resulting total vehicle mass can be used as a mass budget.
----------------------------------
Result for engine-poor mission, delivering 50 ktons propellant
with 15,137 tonnes margin extra
The engine-poor mission would deliver 50,000 tons to a HEEO. One would use aerobrake over many orbital passes to drop the apoapsis of the orbit down to close to LEO. One would then have 50,000 tons at LEO. The engine-poor mission has about 15,138 tons extra propellant left over for margin. It needs a peak power of about 12,142 Megawatts.
|
|
15,137.86 |
tonnes |
Margin excess propellant at destination |
|
minEnginePwr |
watts |
thermal Engine Power |
|
|
Timed Thrust missions |
|
|
|
|
10 |
hours |
copied thrust time |
|
|
|
|
first part |
|
|
|
|
go from Deimos to apoapsis HEMO of Oberth maneuver orbit |
|
|
299030.6299 |
tonnes |
Starting Mass |
|
|
497 |
m/s |
go up from Deimos to HEMO apo |
|
|
305 |
m/s |
at apoapsis go down to LMO |
|
|
|
|
|
|
|
802 |
m/s |
first part dV |
|
ef |
0.34995888 |
|
1 - exp ( - dV / Vsp ) |
|
|
104648.4243 |
tonnes |
propellant mass |
|
|
194382.2056 |
tonnes |
final mass |
|
|
|
|
|
|
|
|
|
second part |
|
|
|
|
dV at HEMO periapsis for Oberth to Mars-Earth Hohman trajectory |
|
|
194382.2056 |
tonnes |
mass at start of maneuver |
|
|
1279.5 |
m/s |
Oberth dV+margin % for Earth Hohman xfr |
|
ef |
0.496999613 |
|
1 - exp ( - dV / Vsp ) |
|
|
96607.88095 |
tonnes |
propellant mass |
|
|
97774.32465 |
tonnes |
final mass |
|
|
|
|
|
|
|
2683.552249 |
kg/sec |
mass flow rate |
|
minSloPwr |
watts |
thermal nozzle power |
|
|
minEnginePwr |
12,142,429,872.71 |
watts |
thermal Engine Power |
|
|
|
|
|
|
|
|
|
third part |
|
|
|
|
Capture into HEEO at Earth |
|
|
97774.32465 |
tonnes |
mass at start of maneuver |
|
|
752.04 |
m/s |
Oberth dV+margin% for Earth HEEO capture |
|
ef |
0.332281293 |
|
1 - exp ( - dV / Vsp ) |
|
|
32488.57907 |
tonnes |
propellant mass |
|
|
65,285.75 |
tonnes |
final mass |
|
|
15,137.86 |
tonnes |
margin payload excess |
|
|
|
|
|
|
|
902.4605296 |
kg/sec |
mass flow rate |
|
|
1646773876 |
watts |
thermal nozzle power |
|
minCapturePwr |
watts |
thermal Engine power |
Credible engines are of the "100 megawatt per ton" type are used, which are credible from an engineering standpoint. Such engines would almost certainly last a century before needing to be refueled. Refueling them would not be the limiting element.
One could use about 322 tones to of the margin propellant 15,137 tons to send the empty water ship back to Deimos from the HEEO.
|
|
322.9643578 |
tonnes |
H2O to send the ship back |
--------------------------
Empty Water Ship sent back to Deimos from LEO
One could send the ship from Low Earth Obit back to Deimos by using 1992 tons of water.
|
|
1992.136979 |
tonnes |
to take the ship back from LEO |
We had delivered about 50,000 tons to HEEO and provided 15,137 tons of margin, some of which is probably available. We then let the payload aerobrake to LEO over many orbital revolutions. The payload then sat at LEO with some of the margin mass.
A separate calculation shows that the reactor power needed to send the empty ship back is tiny compared to that needed to push 50,000 ton (plus margin) payloads. For example, the calculation shows 139 megawatts is the highest power needed to achieve the desired point thrusts.
|
|
1.40E+08 |
watts |
thermal engine power to return to Deimos |
-----------------
Ice Melter
The heat needed to melt ice into water is only about 4.55 megawatts. The ice is assumed to be the payload + propellant, specified as about 299,000 tons per year.
---------------------------------
Uranium mass used to propel water ships
Uranium mass used for propulsion
|
|
|
|
|
2.489E+08 |
kg |
water turned into steam |
|
1.12611E+15 |
Joules |
energy into water |
|
12.7605 |
kg |
Uranium 235 burned per trip |
Nuclear fission (of U-235) (Used in nuclear power plants)
88,250,000 MJ/kg
-----------------------------------
Economics???
If we got $50 per pound for water, and we delivered 50,000 metric tons of it, that would only be about USD $5.5 Billion. That is not a lot of money. It is not a lot of revenue because this is a "small" water tanker. It is "small" because it is only delivering 50,000 tons from a vehicle that is not much more massive (~ 150 tons) than a fully loaded space shuttle (~ 120 tons).
The ship needs a nuclear reactor engine peak power capacity of about 12 Gigawatts. One could imagine paying USD $500 Million total just for the engines, once. I could imagine paying 10 times as much. They would almost certainly be good for a century, 100 years. How do you amortize that?
The tanks and other structures could be just Kevlar bags and struts and such. I don't know how to cost that.
If this whole scheme costs a lot, blame Bush, or Obama, or NASA, or Congress, or the Unions, or maybe France. If it costs too much, ask Zubrin to figure it and then it will cost less. The point is that one must know what to cost before one costs it. This exercise gives us an something to cost.
The water extraction system can be rather simple if you start with hyper-frozen ice mud goop, like you expect to find inside a comet. Some have claimed that's what we expect to find inside Deimos. If you locate the water heater "under" the formation of ice then the water just drips into your tank, ready for you to pump it into the water ship. The water heater is a 4.55 megawatt heater.
In practice, nothing in space is simple.
The water probably has some kind of goo dissolved in it. The goo could either clog the water hoses or will gum up and attack the hyper-hot water heater nuclear reactor elements. The water probably will drip more like cold honey instead of water in the low gravity. Maybe water vapor pressure will build up and blow the whole near earth object to pieces.
Space is mean. Maybe the problem is too hard to solve and we are doomed to stay here on Earth forever, with only terrorists and tax collectors to console us.
Solar vs. Nuclear
One gets about 88.25 million Mega-Joules per kilogram of enriched uranium U235. One gets about 0.001 megajoules per second per square meter of sunlight at the Earth's distance from the sun. Let a Green Peace person figure this one. I estimated that solar powered prospector mission could probably work for a 1 ton payload ship, but only if the solar collector were the best anyone ever estimated.
There just does not seem to be as much complexity in this water scheme compared to the high-tech NASA way, which would have us making cryogenic liquid hydrogen and liquid oxygen.
Someone with more skill than me needs to estimate the costs and economics.
6/29/2010 17:40:01 PM >
mod 2011.07.12_1300
( this
document
in
word format, excel mission
spreadsheet, excel tank spreadsheet
).